Solving quadratic equations is a cornerstone of algebra and a foundational skill in mathematics. The equation “4x^2 – 5x – 12 = 0” presents a unique challenge and learning opportunity. This article delves deep into the techniques and strategies for solving this equation, ensuring that readers come away with a clear understanding and the ability to tackle similar problems.
Understanding Quadratic Equations
Quadratic equations are polynomials of degree two, typically ax^2 + bx + c = 0, where a, b, and c are constants. The x represents the variable or unknown we are trying to solve. These equations are pivotal in various fields, from physics and engineering to finance and statistics.
A clear example is the quadratic equation in focus, 4x^2 – 5x – 12 = 0. Here, a = 4, b = -5, and c = -12. Understanding the structure of quadratic equations is crucial for solving them, as the values of a, b, and c directly influence the solving strategy and the nature of the solutions.
Factoring as a Strategy
Factoring is one of the primary methods used to solve quadratic equations. It involves rewriting the quadratic in a product of two binomials. However, not all quadratics are easily factorable, especially when dealing with more significant coefficients or when the equation does not simplify neatly. Regarding 4x^2 – 5x – 12 = 0, factoring can be challenging due to the coefficients involved. Nevertheless, one can uncover the factors that solve the equation with some practice and technique.

The Process of Factoring
Factoring aims to find two numbers that multiply to give the product of a and c and add to provide b. For our equation, we look for two numbers that multiply to (4)(-12) = -48 and add to -5. This step requires trial and error but is facilitated by a strong understanding of the number of properties and factors.
Once the appropriate numbers are found, the equation is rewritten in a factored form, which can then be set to zero to solve for the values of x. This method is highly effective for easily factorable equations, providing a quick and straightforward solution.
The Quadratic Formula: A Universal Solver
When factoring is too cumbersome or impossible, the quadratic formula offers a fail-safe solution. This formula, x = [-b ± √(b^2 – 4ac)] / 2a, works for any quadratic equation. It directly utilizes the coefficients a, b, and c to find the solutions of x.
Applying the Quadratic Formula to 4x^2 – 5x – 12 = 0
To solve 4x^2 – 5x – 12 = 0 using the quadratic formula, we substitute the values of a, b, and c into the formula. This process demystifies the equation, turning it into a straightforward calculation. The beauty of the quadratic formula lies in its universality and reliability, ensuring that even the most complex equations can be solved.
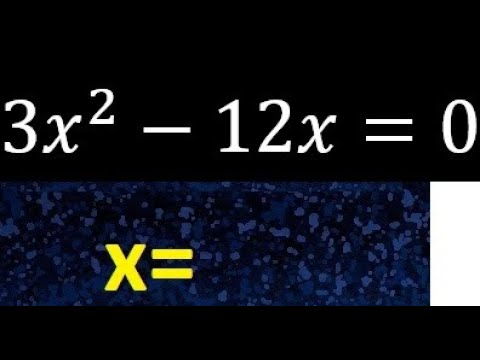
Completing the Square: An Alternate Route
Completing the square is another technique for solving quadratic equations. It involves transforming the equation into a perfect square trinomial, from which the value of x can be easily derived. This method is beneficial for understanding the quadratic formula’s derivation and solving equations when other methods are more complex.
How to Complete the Square
Completing the square requires rearranging and manipulating the equation so that the left side becomes a perfect square. The equation 4x^2 – 5x – 12 = 0 involves:
- Dividing by the leading coefficient (if not 1).
- Moving the constant term to the other side.
- Adding a specific value to both sides to create a perfect square trinomial.
This method finds the solution and offers insight into the equation’s structure.
Graphical Solutions: Visualizing the Equation
Graphing is a powerful tool for visualizing and solving quadratic equations. Plotting the equation on a coordinate plane allows one to see the parabola it forms and identify its roots—the points at which it intersects the x-axis.
Solving 4x^2 – 5x – 12 = 0 Graphically
To solve our equation graphically, one would plot y = 4x^2 – 5x – 12 and look for the x-values where y equals zero. This approach provides a visual understanding of the solutions and the behavior of quadratic functions, complementing the algebraic techniques.
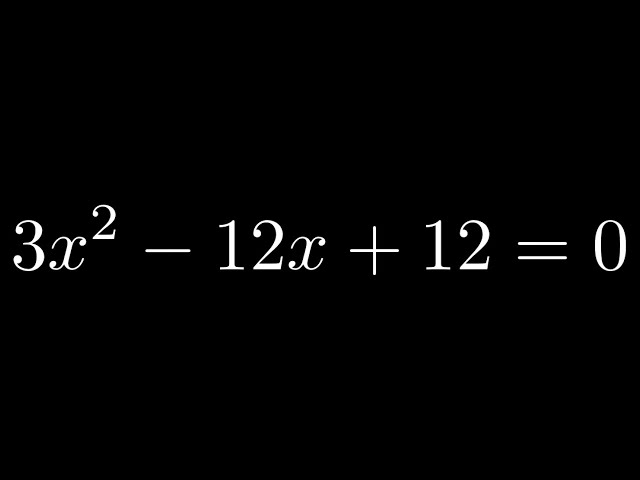
In Conclusion
The quadratic equation 4x^2 – 5x – 12 = 0 offers a rich opportunity to explore various solving strategies, from factoring and the quadratic formula to completing the square and graphical methods. Each technique has strengths and contexts where it is most valuable, providing learners with a versatile toolkit for tackling quadratic equations. Understanding and applying these methods enhances one’s mathematical problem-solving skills, opening doors to further exploration and application in numerous fields. Whether you’re a student, educator, or just curious, mastering these strategies is a step toward a deeper appreciation of mathematics and its practical utility in solving real-world problems.